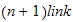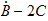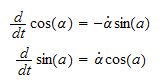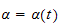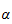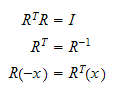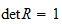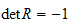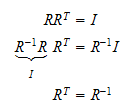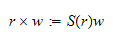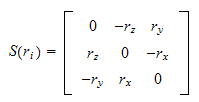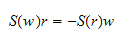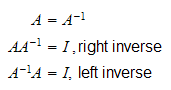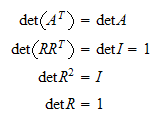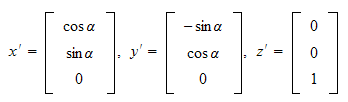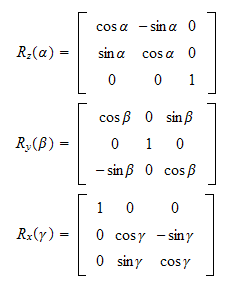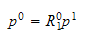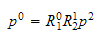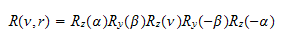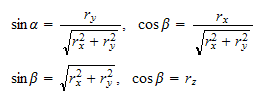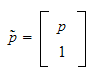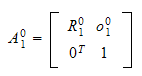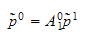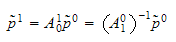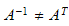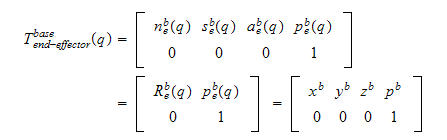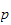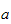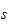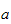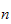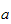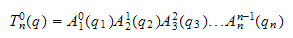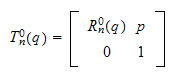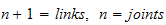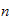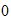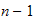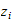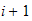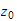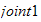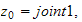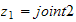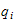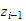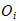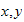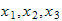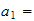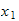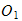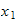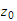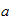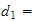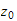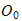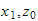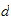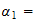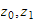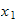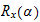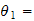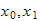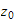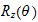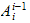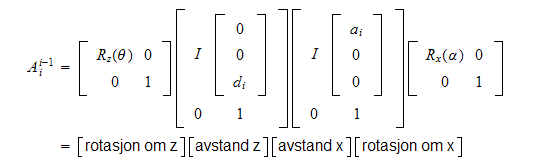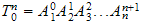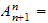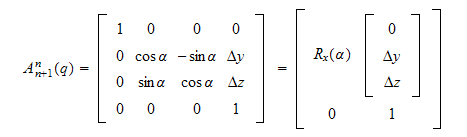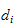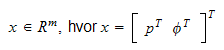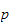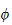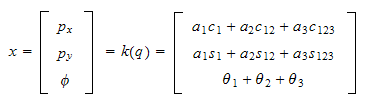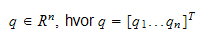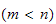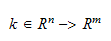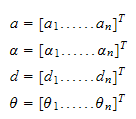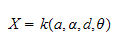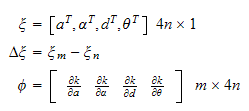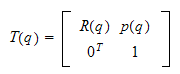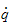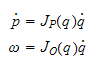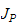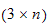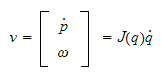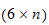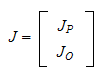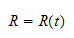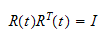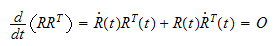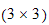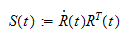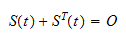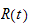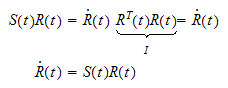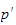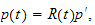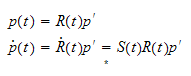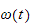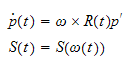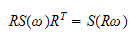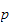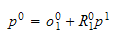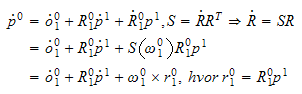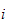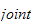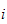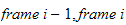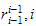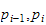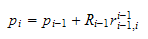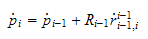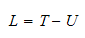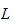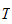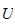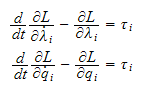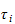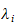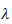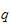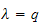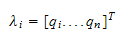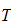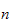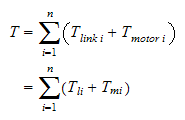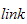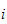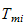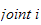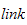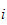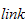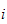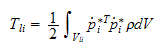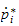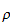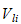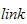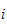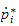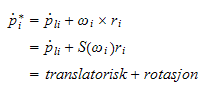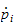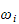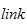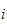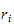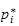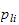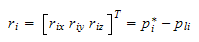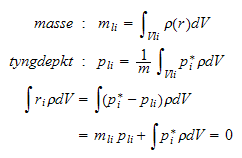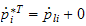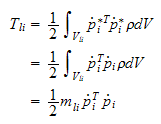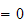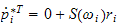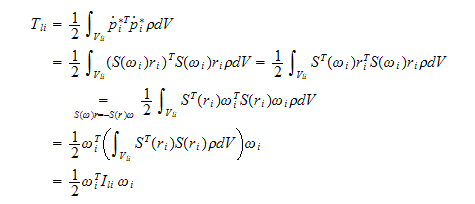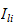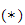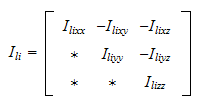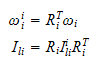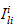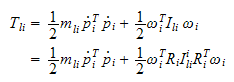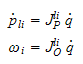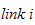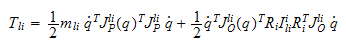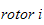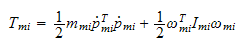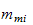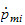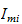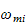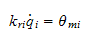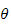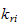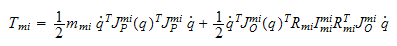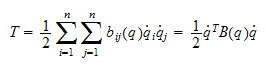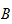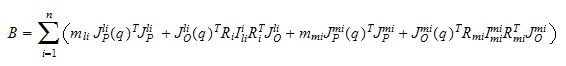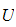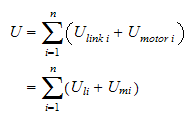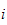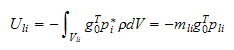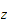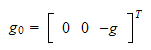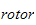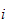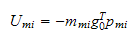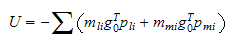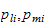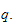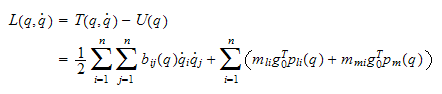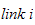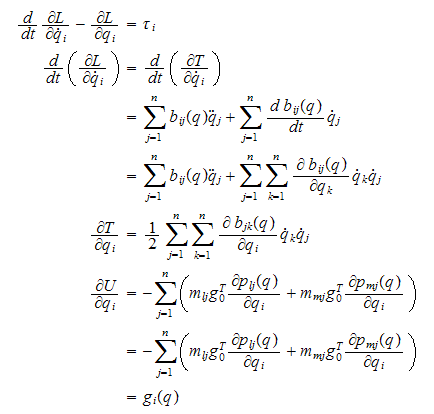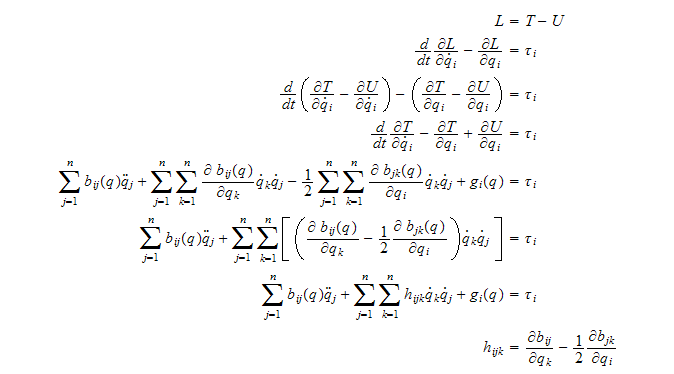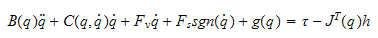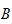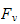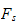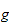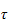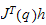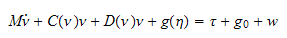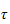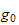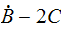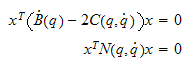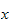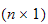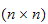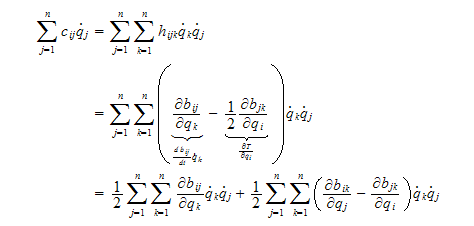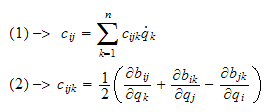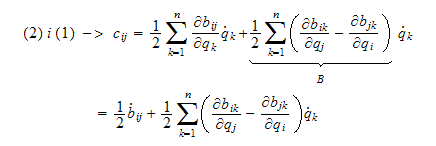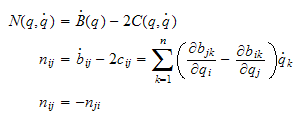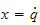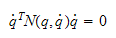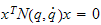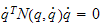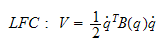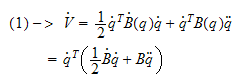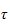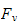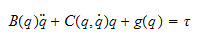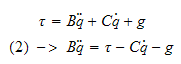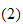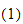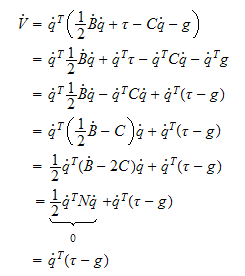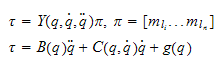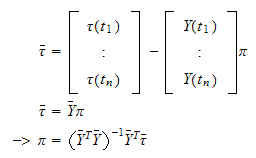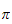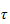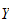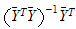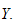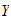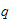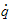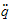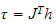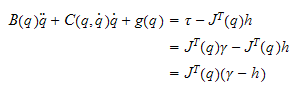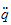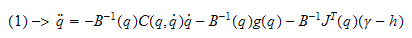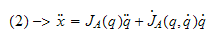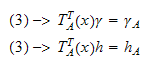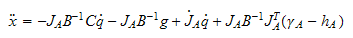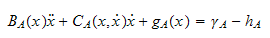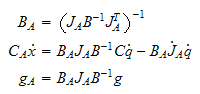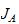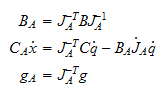formålet med dette dokumentet er at det skal gi et overblikk over
pensumet, slik at det blir mye lettere å lese til muntlig eksamen,
også lettere å bla tilbake i senere tid, samt et sammendrag fra
forelesningene til Svein Ivar Sagatun.
Ordbok
link = arm
joint = ledd
frame = ramme
joint space = leddrommet
operational space = oppgaverommet
TCP = Tool Centre Point
End-effector = samme som TCP, enden/tuppen av robotarmen
redundans = overskudd (av krefter, ledd,,) samme som overaktuert system
åpen kinematisk sløyfe
lukket kinematisk sløyfe
singularitet
Eksamenstips
Kapitler merket med * er oppgaver som kan dukke opp
på eksamen...
-
Finne "resten" av rotasjonsmatrisa
-
DH-konvensjonen, kan vi ikke denne er det garantert stryk
-
må kunne sette opp DH og måle seg frem til dataene til TCP
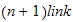
-
Fullt bevis med Lyapunovanalyse, se smørbrødsliste i kap5.
-
Skal vite hvordan man kommer frem til skjevsymmetrisk matrise
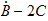
-
medsensor er ofte Fjellstad fra Sitex
-
Hvis vi ikke kan så mye, spør Fjellstad om grunnleggende
reguleringsteknikk (sikkert PID-regulatorer, stabilitet, fasemargin osv..).
Prosjektoppgave tips
-
Formålet er å "selge" rapporten til leseren/professoren
-
Plott mange plott i samme vindu - lett å sammenlikne da
-
Skal være lett å lese, ikke bla frem og tilbake og lete etter
figurer, osv
Forelesninger
Introduction to the course and robotics in general.
Kinematics
Denavit Hartenberg convention
Denavit Hartenberg
Differential kinematics
Dynamics and some differential kinematics.
Dynamics, Trajectories and Motion Control.
Kap 2 - *Kinematikk
Sammendrag: Handler om rotasjonsmatriser, vektorer, direkte kinematikk,
Denavit-Hartenberg konvensjonen
Derivasjon
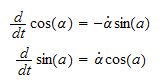
hvor
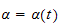 ,
dvs
,
dvs
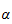 er en funksjon av tiden (derfor derivert av kjernen)
er en funksjon av tiden (derfor derivert av kjernen)
2.2 2.3 Om rotasjonsmatriser
egenskaper til
rotasjonmatrisen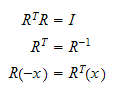
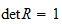 er høyrehåndssystem, og
er høyrehåndssystem, og
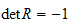 er venstrehåndssystem
er venstrehåndssystem
Rotasjonsmatrisen mellom to rammer er et element av
 spesiell
ortogonal gruppe av
3.orden
spesiell
ortogonal gruppe av
3.orden
et lite
bevis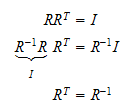
litt mer om ortogonalitet...
Skjevsymmetriske matriser
se kap 4.1.1
kryssproduktet til en vektor er definert
som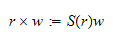
da er den skjevsymmetriske
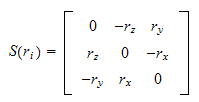
egenskap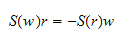
Inverse matriser
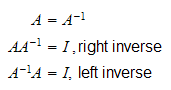
venstre og høyre invers eksisterer kun hvis A har full rang. Hvis A er
singulær (mister rang, det=0) eksisterer ikke den inverse.
Determinant
regler mht
determinant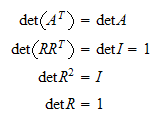
Elementærrotasjoner
Rotasjon om z-aksen
gir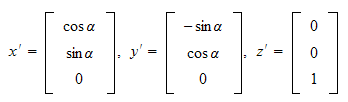
det
gir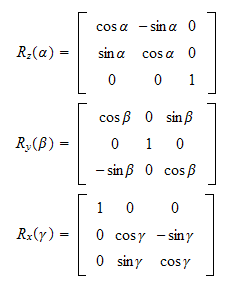
vektor fra et koordinatsystem til et
annet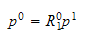
vektor gjennom flere koordinatsystem (eller
robotakser)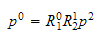
Notation
i robot postmultipliserer man rotasjonmatriser, i navfart premultiplisering,
hvorfor?
Notation
i robot roterer man i forhold til aksene. akse1 vs akse2....
2.5 Rotasjon om en vilkårlig akse (nyttig og praktisk)
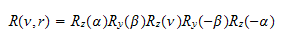
hvor
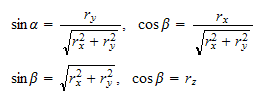
2.6 Kvarternioner (ikke forelest, men pensum?)
ikke forelest, men pensum? SIS har aldri brukt dette i praksis...
2.7 Homogene transformasjoner
relasjonen mellom et punkt i to koordinatsystem (frames), kan utvides med et
fjerde
element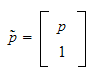
homogen transformasjon (koordinat
transformasjon)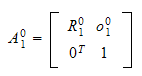
som betyr en transformasjon fra frame 1 til frame 0
Dette kan skrives på en kompakt form
som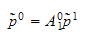
transformasjon fra ramme 0 til ramme 1 er
da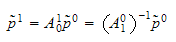
Notation
ikke ortogonal
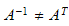
2.8 Direkte kinematikk
Hvor er TCP (tool centre point / end-effector) når vinkler og
utstrekning er gitt?
Dvs vi vet vinklene i hvert robotledd og forskyvning (hvis prismatiske ledd)
Homogen transformasjon gitt i base koordinater (n s a p, normal sliding
approach position)
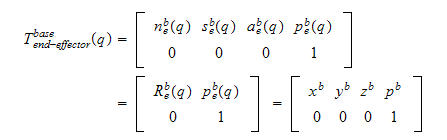
hvor
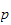 =posisjon
til end-effector,
=posisjon
til end-effector,
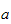 =retning
mot objekt(approach),
=retning
mot objekt(approach),
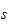 =normal
til
=normal
til
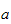 (sliding plane of jaws),
(sliding plane of jaws),
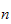 =normal
til
=normal
til
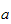 og
og
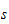 slik at systemet er høyre-hånd. Ta pistolgrepet, a pekefinger, s
langfinger, n tommel (tilsvarende x,y,z koordinater)
slik at systemet er høyre-hånd. Ta pistolgrepet, a pekefinger, s
langfinger, n tommel (tilsvarende x,y,z koordinater)
Total transformasjon blir
da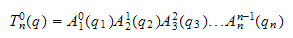
som er rekursivt
2.8.2 *Denavit-Hartenberg konvensjonen
mål: skal
finne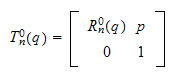
antar
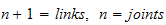
-
Nummerer alle armledd (joints) fra
 til
til
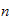 -> n=1,2,3,4,5,6,7
-> n=1,2,3,4,5,6,7
-
(Finn og nummerer jointaksene fra
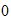 til
til
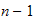 -> joint1 er akse0, joint2 er akse1)
-> joint1 er akse0, joint2 er akse1)
-
Velg
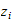 langs
aksen til joint
langs
aksen til joint
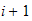 ,
dvs
,
dvs
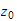 peker langs
peker langs
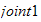 , ->
, ->
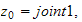
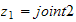
->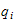 roterer/translaterer om
roterer/translaterer om
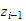 aksen.
aksen.
-
Lokaliser origo
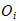 ,
og finn
,
og finn
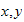 slik at man får et høyrehåndssystem. x er normalen til
z-planet. Lurt å velge en akse som har samme retning i alle rammene (eks.
slik at man får et høyrehåndssystem. x er normalen til
z-planet. Lurt å velge en akse som har samme retning i alle rammene (eks.
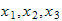 .. peker alle i samme retning = parallelle).
.. peker alle i samme retning = parallelle).
-
Lag
DH-tabell

les:
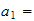 avstand
langs
avstand
langs
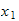 fra
fra
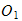 til krysset
til krysset
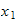 ,
,
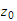 ->avstand fra joint1 til forrige joint langs x1, avstand i x =
->avstand fra joint1 til forrige joint langs x1, avstand i x =
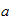
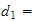 avstand
langs
avstand
langs
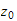 fra
fra
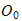 til krysset
til krysset
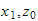 ->avstand fra joint1 til forrige joint langs z0, avstand i z =
->avstand fra joint1 til forrige joint langs z0, avstand i z =
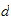
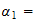 vinkel
mellom
vinkel
mellom
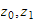 om
om
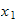 -> vinkel mellom joint1 og forrige om x-aksen, Rotasjon om x,
-> vinkel mellom joint1 og forrige om x-aksen, Rotasjon om x,
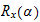
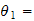 vinkel
mellom
vinkel
mellom
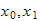 om
om
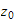 -> vinkel mellom joint0 og forrige om z-aksen, Rotasjon om z,
-> vinkel mellom joint0 og forrige om z-aksen, Rotasjon om z,
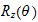
-
Finn den homogene transformasjonen
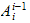
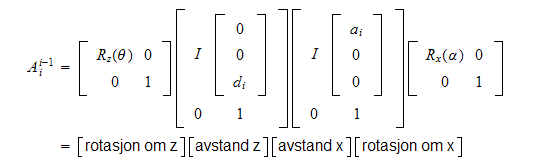
-
Finn total transformasjon
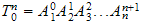
-
Finn verktøytransformasjon
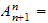 konstant
konstant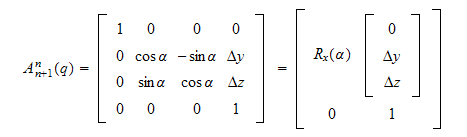
Notation
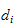 er egentlig en offset pga tykkelse i robotarm.
er egentlig en offset pga tykkelse i robotarm.
Notation
Bra å designe robot uten offset, mye enklere da
Notation
Lurt med mest mulig parallelle akser
2.10 oppgaverommet og leddrommet
Oppgaverommet er definert som
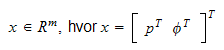
hvor
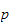 er posisjonen til TCP og
er posisjonen til TCP og
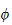 er dens orienteringen
er dens orienteringen
Eks med to-planar-link
robot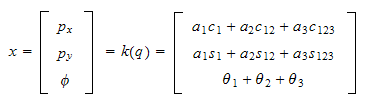
Leddrommet er definert
som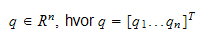
2.10.1 Workspace
Det arbeidsområdet TCP kan nå.
2.10.2 Kinematisk redundans
En robot er kinematisk redundant når den har flere frihetsgrader av
mobilitet enn variabler som trengs for å utføre en bestemt oppgave.
Hvis dimensjonen i oppgaverommet er mindre enn dimensjonen i leddrommet
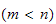 så er roboten kinematisk redundant. Redundans er relativ i forhold til
den oppgaven roboten skal utføre. En 6akse robot er funksjonelt
redundant, men ikke intrinsically redundant.
så er roboten kinematisk redundant. Redundans er relativ i forhold til
den oppgaven roboten skal utføre. En 6akse robot er funksjonelt
redundant, men ikke intrinsically redundant.
2.11 Kinematisk
kalibrering (ikke ferdig forklart her)
Nyttig i praksis, dårlig beskrevet i boka.
Definition
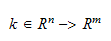
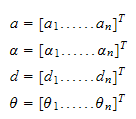
Definition
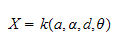
Definition

Definition
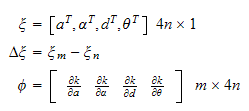
2.12 Invers kinematikk
Hva er leddvinklene hvis vi har en gitt TCP og orientering?
Gitt TCP og orientering. Hvordan blir vinklene da?
Man designer dette analytisk, ønsker ikke numeriske verdier.
Foreleser hoppet over dette tema på forelesing, fordi det var
så fryktelig kjedelig. Pensum?
Kap 3 - Differensiell kinematikk og statikk
3.1 Geometrisk Jacobi
Direkte kinematikk skrives som en homogen
transformasjonsmatrise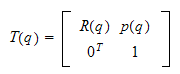
Målet med differensiell kinematikk er å finne sammenhengen mellom
leddhastighetene og end effector lineær- og rotasjonshastighet. Med andre
ord, vi skal finne den linære hastigheten til TCP
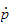 ,
og rotasjonshastigheten
,
og rotasjonshastigheten
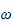 som en funksjon av leddhastighetene
som en funksjon av leddhastighetene
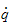 med følgende
likninger
med følgende
likninger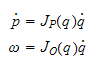
hvor
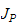 er en
er en
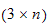 matrise relativt til bidragret fra leddhastigheten
matrise relativt til bidragret fra leddhastigheten
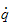 til TCPs lineære hastighet
til TCPs lineære hastighet
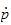
og
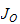 er en
er en
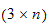 matrise relativt til bidragret fra leddhastigheten
matrise relativt til bidragret fra leddhastigheten
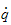 til TCPs angulære (vinkel) hastighet
til TCPs angulære (vinkel) hastighet
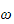
som kompakt kan skrives
som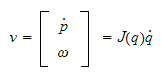
Dette representerer robotens differensielle kinematiske likninger.
Den geometriske jacobien
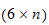 er
da
er
da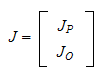
3.1.1 Tidsderivering av rotasjonsmatrise
En tidsvarierende rotasjonsmatrise
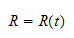
med ortogonal egenskap
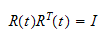
som derviveres med hensyn
på tiden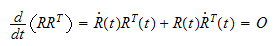
definerer den skjevsymmetriske
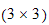 matrisen
S
matrisen
S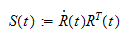
og er skjevsymmetrisk
fordi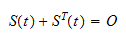
Postmultipliserer begge sider av
* med
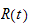
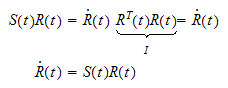
Hvis vi deriverer en konstant vektor
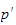 og vektoren
og vektoren
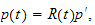 får
vi
får
vi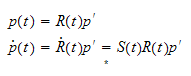
Hvis vi deriverer en angulær vektor
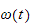 ,
får
vi
,
får
vi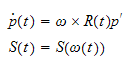
Hvis R er en
rotasjonsmatrise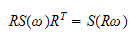
eksempel 3.1, likn
* tidsderiveres og settes inn i *
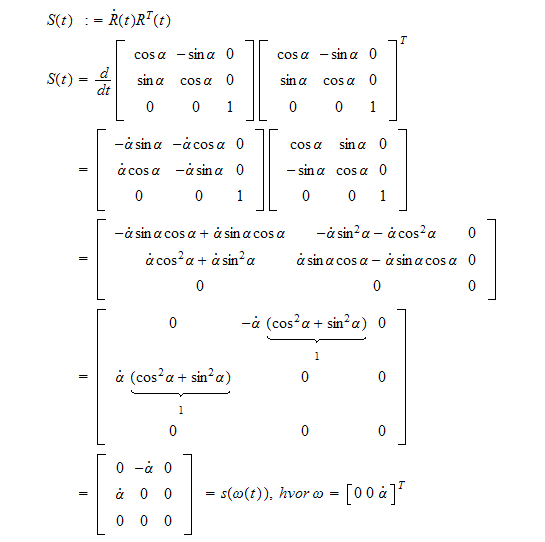
Dette uttrykker rotasjonshastigheten for rammen om z-aksen.
eks. figur 2.11 i bok.
vi skal transfomere ett punkt
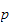 ,
fra ramme 1 til ramme
0
,
fra ramme 1 til ramme
0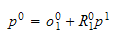
denne
tidsderiveres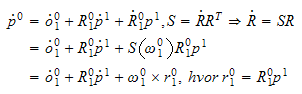
Notation
husk postmultiplisering i robotverden
3.1.2 Armledd hastighet (linkhastighet)
Betrakt en generell
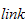
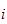 i en robot med en åpen kinematisk sløyfe. I følge
DH-konvensjonen, beskriver
i en robot med en åpen kinematisk sløyfe. I følge
DH-konvensjonen, beskriver
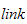
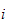 forbindelsen mellom
forbindelsen mellom
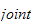
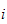 og
og
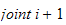 .
(ledd i og ledd i+1).
.
(ledd i og ledd i+1).
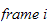 er festet til
er festet til
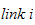 med origo langs aksen
med origo langs aksen
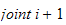 ,
og
,
og
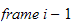 har origo langs
har origo langs
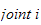 aksen. (Se fig 3.1 s 82 i bok)
aksen. (Se fig 3.1 s 82 i bok)
Vi lar posisjonsvektorene
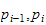 gå fra baseramme
gå fra baseramme
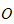 til
til
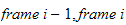 .
Vi danner en trekant med posisjonsvektoren
.
Vi danner en trekant med posisjonsvektoren
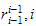 ,
som er avstanden mellom
,
som er avstanden mellom
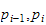 .
Da kan vi skrive koordinattransformasjonen
* som
.
Da kan vi skrive koordinattransformasjonen
* som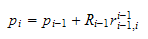
som
deriveres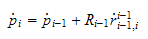
3.1.3 Beregning av Jacobi
3.2.1 Eksempel beregning av jacobi på en tre-link planar arm
3.3 Kinematisk singularitet
Når jacobien ikke er inverterbar, og mister rang oppstår
singularitet. Det=0
se eks fig3.3 i boka.
Når armene er helt utstrekt/sammentrekt (boundary singullarities),
så kan vi ikke spesifisere en vilkårlig hastighet/posisjon der vi
ønsker.
3.4 Analyse av redundans
3.5 Invertert differensialkinematikk (Differential Kinematics Inversion)
3.5.1 Redundante systemer
3.6 Analytisk jacobi
3.7 Inverse kinematiske algoritmer
3.8 *Statikk (typisk eksamensstoff)
Kap 4 - Dynamikk
Å utvikle en dynamisk modell for en manipulator, spiller en viktig rolle
for å simulere bevegelse (motion), analyse av struktur til roboten og
design av reguleringsalgoritmer. Simulering av bevegelse gjør at man kan
prøve ut reguleringstrategier og teknikker for bevegelsesplanlegging uten
å bruke et fysisk system. Analyse av dynamisk modell kan være god
hjelp til mekanisk design av prototyper. Berekninger av krefter og momenter
for å oppnå typisk ønskede bevegelser gir verdifull informasjon
om å designe ledd (joints), transmisjoner og aktuatorer.
Kapittelet tar for seg to metoder for å berekne bevegelseslikningene til
en robot i leddrommet (joint space).
-
Lagrange - forholdsvis enkelt og systematisk modellering, bruker generaliserte
koordinater
-
Newton-Euler - Rekursiv modellutvikling, effektivt siden man studerer den
typiske åpne strukturen i robotens kinematiske kjede.
4.1 Lagrange
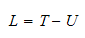
hvor
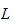 =
total energi,
=
total energi,
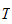 = total kinetisk energi,
= total kinetisk energi,
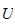 = total potensiell energi i generaliserte koordinater
= total potensiell energi i generaliserte koordinater
Lagrange's
likning: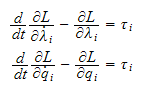
som beskriver endringen i energien og
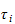 = generaliserte krefter og
= generaliserte krefter og
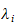 generaliserte
koordinater
generaliserte
koordinater
Et naturlig valg av generaliserte koordinater
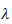 for en robot er leddvinklene
for en robot er leddvinklene
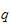 ,dvs
,dvs
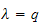
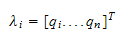
4.1.1 Beregning av kinetisk energi 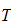
Vi har en manipulator med
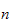 stive armledd. Total energi finnes ved å summere opp bidraget fra
bevegelsen til hvert armledd og hvert
motor/aktuator-ledd.
stive armledd. Total energi finnes ved å summere opp bidraget fra
bevegelsen til hvert armledd og hvert
motor/aktuator-ledd.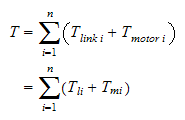
hvor
 er kinetisk energi i armledd
er kinetisk energi i armledd
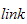
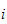 ,
og
,
og
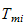 er kinetisk energi i motor som virker på ledd
er kinetisk energi i motor som virker på ledd
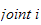
Kinetisk energi fra
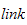
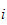 ,
armledd
,
armledd
Kinetisk energi fra
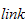
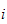 er gitt
av
er gitt
av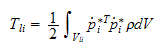
hvor
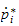 er lineær hastighetsvektor og
er lineær hastighetsvektor og
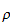 er tetthet, summert opp over
er tetthet, summert opp over
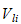 som er volumet av armleddet
(
som er volumet av armleddet
(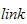
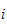 ).
).
Hastigheten til punktet
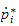 kan finnes ved skjevsymmetrisk
matrise
kan finnes ved skjevsymmetrisk
matrise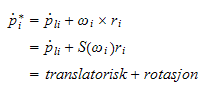
hvor
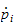 er hastigheten i massesenteret, og
er hastigheten i massesenteret, og
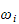 er rotasjonshastigheten om massesenteret til armleddet
(
er rotasjonshastigheten om massesenteret til armleddet
(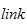
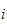 ),
),
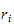 er en forskjellen mellom posisjonsvektorene
er en forskjellen mellom posisjonsvektorene
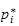 og
og
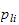
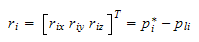
noen viktige
formler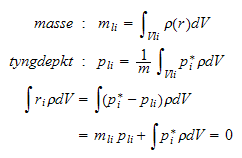
Ved å substituere * inn i
*, kan vi finne kinetisk energi i hvert ledd.
De forskjellige bidragene er gitt ved:
-Translatorisk, null rotasjon, gir
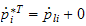
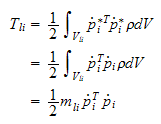
-Mutual
(innbyrdes, felles, gjensidig)
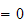 ,
hva er dette for ett bidrag?
,
hva er dette for ett bidrag?
-Rotasjon, med lineær hastighet lik null,
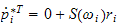
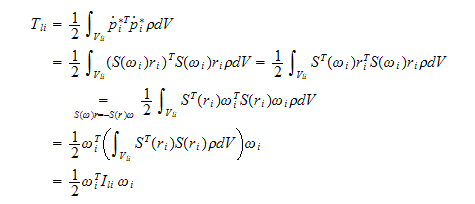
hvor treghetsmatrisen
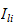 er symmetrisk
er symmetrisk
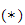
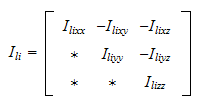
Treghetsmatrisen er gjelder om massesenteret til den aktuelle linken
(armleddet).
Ved bruk av DH-konvensjonen vil rotasjonsleddet
være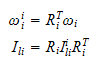
fordi det går fra ramme til ramme.
Hvis en befinner seg i samme ramme som armleddet, blir
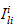 konstant.
konstant.
Ved summasjon av translatorisk * og
rotasjons energi *, får
vi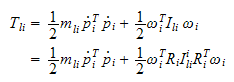
Nå må vi uttrykke den kinetiske energien som en funksjon av de
generaliserte koordinatene til systemet, som er leddvinklene. Vi bruker
den geometriske metoden for å berekne Jacobien til de
mellomliggende armleddene.
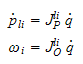
Da blir den endelige summen for kinetisk energi fra
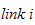
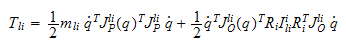
Kinetisk energi fra motor
Man bruker samme fremgangsmåte som over.
Kinetisk energi for
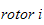 kan skrives
som
kan skrives
som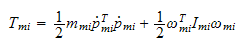
hvor
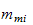 er
massen til rotoren,
er
massen til rotoren,
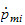 er massesenterets lineære hastighet til rotoren,
er massesenterets lineære hastighet til rotoren,
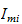 er treghetsmomentet om rotorens massesenter og
er treghetsmomentet om rotorens massesenter og
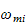 er vinkelhastigheten til rotoren.
er vinkelhastigheten til rotoren.
Man kan også innføre gir som reduserer
energien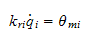
hvor
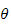 er vinkelposisjon og
er vinkelposisjon og
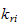 er girreduksjonsforholdet
er girreduksjonsforholdet
Total kinetisk energi for motor blir til slutt som i
* (etter å ha hoppet
over en del
likninger)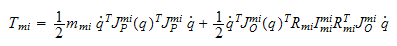
Sum kinetisk energi
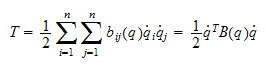
hvor
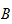 er treghetsmatrisen, symmetrisk, positiv
definitt
er treghetsmatrisen, symmetrisk, positiv
definitt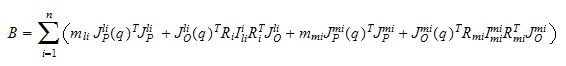
4.1.2 Beregning av potensiell energi 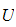
Som for kinetisk energi, så er potensiell energi som er lagret i roboten,
gitt ved en sum av bidrag mellom hver link ( også mellom hver
rotor).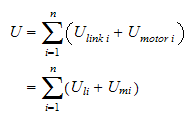
Man antar også her stive armledd (hvis ikke må man ta med elastiske
krefter for fleksible ledd - eks hvis en robot går uhyre fort, får
den en "slangeliknende" bevegelse)
Potensiell energi
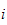
Det er kun gravitasjonen som bidrar med potensiell energi, dermed får
vi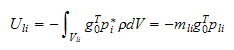
gravitasjonsvektoren (med
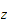 som vertikalakse) kan f.eks velges
som
som vertikalakse) kan f.eks velges
som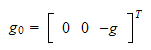
Potensiell energi
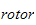
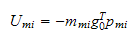
Sum potensiell energi
summerer likn * og
*
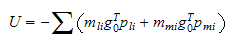
merk at den potensielle energien kun virker gjennom posisjonsvektorene
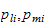 .
, og ikke gjennom leddhastigheten
.
, og ikke gjennom leddhastigheten
 slik som med kinetisk energi. Dermed er potensiell energi kun en funksjon av
leddvariablene
slik som med kinetisk energi. Dermed er potensiell energi kun en funksjon av
leddvariablene
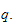
4.1.3 Bevegelseslikninger
Når vi har bereknet den totale kinetiske og potensielle energien til
roboten, kan vi skrive Lagrangelikningen *
som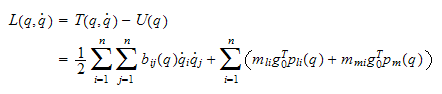
Lagrangelikn * deriveres mhp leddhastigheten
til
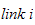 ,
(husk at
,
(husk at
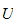 ikke er avhengig av
ikke er avhengig av
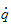 )
)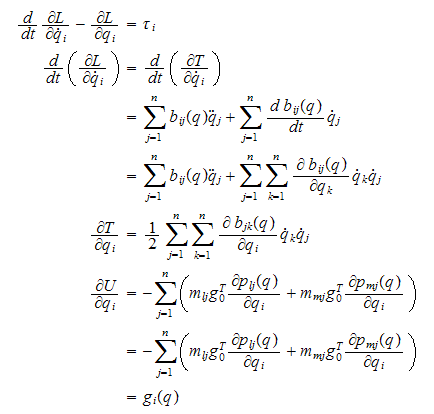
bevegelseslikningene blir dermed
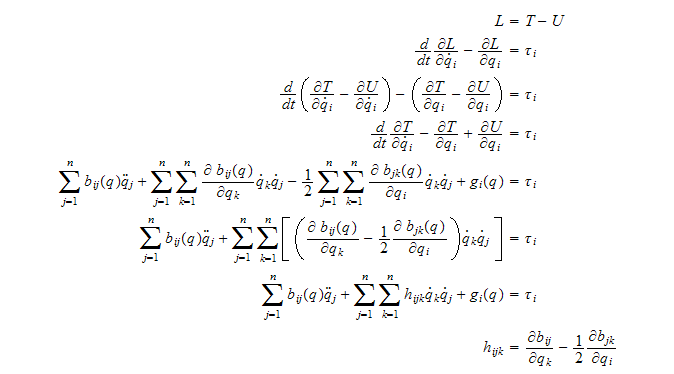
forstår ikke hvordan man deriverer med summetegn
Resultat: Dynamisk modell i leddrommet
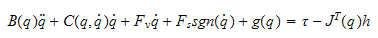
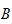 er treghetsmatrise ,
er treghetsmatrise ,
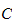 korioles,
korioles,
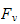 viskøs friksjon,
viskøs friksjon,
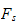 coloumb
friksjon,
coloumb
friksjon,
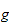 gravitasjon,
gravitasjon,
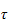 ytre krefter,
ytre krefter,
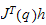 indusert moment fra end-effector
indusert moment fra end-effector
Tilsvarende matrise i marine-språk er
(Fossen)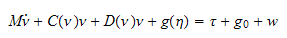
hvor M er systemets treghetsmatrise, C coriolis-centripetal matrise, D
dempematrise, g gravitasjonsvektor,
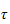 control inputs,
control inputs,
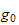 vektor for pretrimming, w vektor for forstyrrelse som vind, bølger,
strøm.
vektor for pretrimming, w vektor for forstyrrelse som vind, bølger,
strøm.
4.2.1 *Skjevsymmetriske matrise 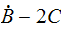
Skal
bevise: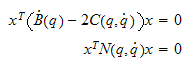
hvor
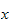 er en hvilken som helst
er en hvilken som helst
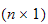 vektor.
vektor.
C
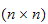 matrisa skrives
som
matrisa skrives
som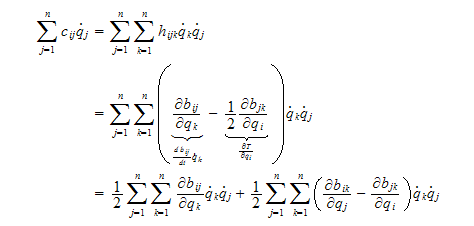
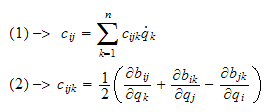
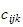 er Christoffel symbol of the first type, pga symmetri i
er Christoffel symbol of the first type, pga symmetri i
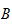 så er
så er
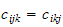 .
.
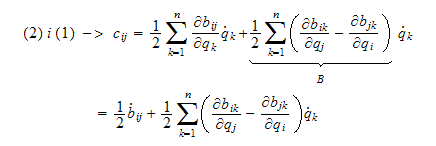
videre har
vi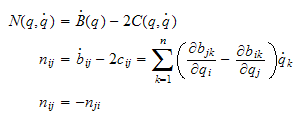
hvis vi setter
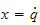 så får vi
så får vi
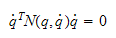
som ikke er det samme som
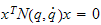 ,
fordi
,
fordi
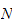 inneholder
inneholder
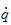 .
.
For å bevise at påstand
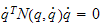 ,
er riktig så må vi bruke Lyapunovanalyse.
,
er riktig så må vi bruke Lyapunovanalyse.
Lyapunovbevis: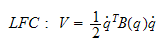
som
deriveres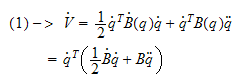
vi velger en passende "høyreside"
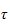 fra likn * (med null friksjon
fra likn * (med null friksjon
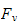 )
)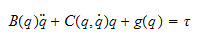
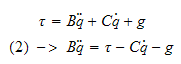
setter inn
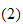 i
i
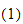
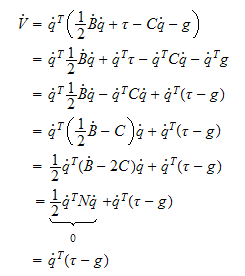
som blir
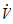
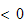 hvis
hvis
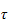 velges mindre enn
velges mindre enn
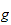
4.3 Gir tre eksempler på dynamisk modellering
(ikke forelest)
-
Two-link cartesian arm
-
Two-link planar arm
-
Paralellogram-arm
4.4 Dynamisk parameter identifikasjon
Å berekne de dynamiske parametrene ut fra en mekanisk modell er ikke
trivielt. For å estimere parametrene bruker vi teknikker fra
systemidentifisering. (Se kinematisk kalibrering)
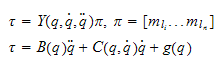
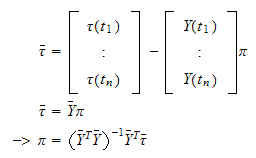
vi kan beregne parametervektoren
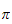 fra målinger av leddvinkelmomentet
fra målinger av leddvinkelmomentet
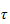 og evaluering av matrisen
og evaluering av matrisen
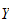 med en minste-kvadraters
metode
med en minste-kvadraters
metode
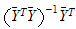 er venstre-pseudo-invers av matrisen
er venstre-pseudo-invers av matrisen
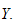
Forutsetninger:
-
Vi antar at de kinematiske parametrene i
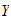 er kjent, f.eks etter en kinematisk kalibreringsprosedyre
( *)
er kjent, f.eks etter en kinematisk kalibreringsprosedyre
( *)
-
posisjonsmåling av vinkel
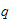
-
hastighetsmåling av vinkel
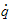
-
akselerasjon av vinkel
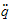 (numerisk beregnet)
(numerisk beregnet)
4.7 Operational Space Dynamic model (oppgaverommet)
Som et alternativ til leddrom-modellen, kan bevegelseslikningene til roboten
uttrykkes direkte i oppgaverommet. Vi må da finne en dynamisk modell som
beskriver forholdet mellom de generaliserte kreftene som virker
på roboten og variablene som beskriver TCP posisjonen og orienteringen i
oppgaverommet (operational space).
Vi starter med den dynamiske likningen i leddrommet
* og antar null friksjon
vi setter
også 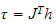 fordi
(se likn 3.99 i bok fra
statikkkapittelet)
fordi
(se likn 3.99 i bok fra
statikkkapittelet)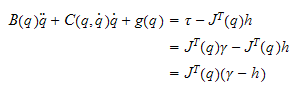
og snur denne mhp akselerasjonen
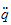
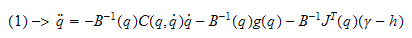
hvor likningen inneholder den geometriske jacobien.
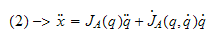
hvor denne likningen inneholder den analytiske jacobien.
Derfor må vi lage en transformasjon mellom de to jacobiene
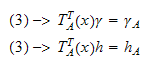
Ved å substituere (1) inn i (2), og bruke transformasjonen i (3),
får
vi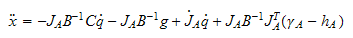
Som kompakt kan skrives
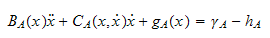
hvor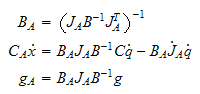
gjelder for en ikke-redundant robot og
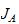 må ha full rang.
må ha full rang.
For reduntant robot gjelder
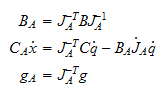
Kap 5 - Trajektorplanlegging
se artikkel til SIS
Kap 6 - Motion Control
6.2 Joint Space Control
6.3 Independent Joint Control (ikke forelest - men i høyeste grad pensum)
6.5 Centralized Control